PROGRESO CIENTÍFICO Y APROXIMACIÓN A LA VERDAD (5)

Recordemos la "reconstrucción" que en la anterior entrada de la serie había propuesto para la noción intuitiva de "grado en el que nos parece que una teoría T se ha aproximado a la verdad, a la luz de los datos empíricos E"
.

Vs(T,E) = p(T,E)/p(TvE).

.

Como indicaba al final, esta fórmula (que, además, se puede modificar para tener en cuenta el carácter aproximado de E, y el hecho de que está constituída por numerosas regularidades empíricas independientes entre sí) posee propiedades de lo más interesante. Pero antes de enumerarlas, indiquemos cuál es el objetivo principal de tener una definición como ésta: se trata de tener una reconstrucción matemática de los criterios comparativos que nos permiten decir si una teoría nos parece mejor que otra, o si una teoría nos parece en cierto momento mejor o peor que lo que nos parecía antes.
.
Bueno, pues vamos con las propiedades. En la próxima (y supongo que última, o penúltima) entrada, comentaré algunas implicaciones más "filosóficas" que también creo que son interesantes.
.
1) La probabilidad de una tautología es siempre igual a 1 (pues p(Taut, E) y P(Taut v E) siempre son 1, sea cual sea E). Nótese que 1 es un valor "bajo", pues Vs puede tener cualquier valor positivo.
.
2) Si los datos E confirman T, entonces Vs(T,E) = 1/p(T). Esto no suele ser una situación habitual: lo corriente es que busquemos teorías que expliquen los datos, y por lo tanto, una teoría T tales que E se siga de ella, no que T se siga de E. Pero podemos considerar que esto se aplica a cada una de las leyes empíricas cuya conjunción es E; lo que nos dice este resultado es que esas leyes serán tanto más valiosas científicamente cuanto menor sea su probabilidad a priori, es decir, cuanto más inesperadas sean.
.

.
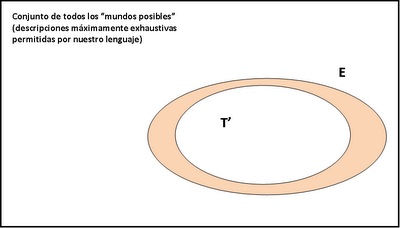
3) Si T explica E (es decir, si E se sigue de T), entonces Vs(T,E) = p(T)/p(E)^2. De aquí se sigue, en primer lugar, que, de dos teorías que consigan explicar E, la que nos parecerá más verosímil es la que es menos implausible a priori. En segundo lugar (o, lo que viene a ser lo mismo), la verosimilitud de una teoría que explica los hechos empíricos es inversamente proporcional a la probabilidad de que E sea verdad y T sea falsa (o sea, p(E&¬T): el área anaranjada en la imagen), o sea, si T está "dentro" de E, entonces cuanto más "espacio" ocupe dentro de E, más verosímil nos parecerá; o sea: cuanto menos espacio quede para teorías que sean incompatibles con E pero que también expliquen E, más verosímil nos parecerá T. Esto puede entenderse como una reconstrucción de la idea de David Deutsch de que las buenas explicaciones son las que resultan "difíciles de variar", pero entendiendo por "variar" la probabilidad de que HAYA algunas otras teorías T' que también expliquen E (probabilidad que es igual al área anaranjada), y no la probabilidad de que NOSOTROS ENCONTREMOS alguna de esas teorías (probabilidad que dependerá de otros factores, no sólo de cómo es el mundo o de cómo nos parece que es). Deutsch creo que confunde ambos sentidos, y eso hace de su explicación del asunto una explicación poco explicativa.
.
Por cierto, este resultado también implica que, para que una teoría T que explica los hechos empíricos E sea mejor que una "explicación tautológica" (cuya verosimilitud, recordemos, era igual a 1), entonces debe cumplirse que p(T,E) > p(E), lo que parece un requisito razonable (es decir, visto al revés, si la probabilidad de que T sea verdadera bajo el supuesto de que E es verdadero, es incluso menor que la probabilidad a priori de que E sea verdadero, entonces es que T es condenadamente mala: es incluso peor que no decir nada).
.
4) Si se confirma una nueva predicción F de la teoría T (es decir, una no incluida en aquellas cuya conjunción es E), entonces su verosimilitud aumenta, es decir, Vs(T,E) < Vs(T,E&F). Esto se cumple tanto si entendemos la "predicción" en el sentido de que T implica F, como en el sentido de que T únicamente implica que, si E es verdad, también es verdad F, como en el sentido de que p(F,T&E) > p(F,T).
.
Una de las propiedades más chorra y que a mí más me gusta es la siguiente:
.
5) Vs(T,E) es siempre menor o igual que 1/p(T) y que 1/p(E). Esta propiedad es importante porque para cada teoría posible, siempre hay un límite a la verosimilitud que puede alcanzar, y para conjunto de datos empíricos, siempre hay un límite a la verosimilitud que pueden conceder a cualquier teoría. Es decir, la ciencia siempre nos presentará situaciones en que lo único que podremos hacer para tener teorías aún más verosímiles que las que tenemos es, o bien inventar teorías cuya plausibilidad a priori sea más baja que la de las teorías anteriores, o bien encontrar nuevos datos empíricos, y generalmente ambas cosas. Esto hace honor a la idea popperiana de que la ciencia es una "búsqueda sin término". Y por otro lado, también nos muestra que la plausibilidad a priori de las teorías (lo "razonables" que nos parezcan, con independencia de los datos empíricos) es un arma de doble filo: según el punto 3 no puede ser muy baja, pero según el punto 5, habrá veces en que tengamos que inventar teorías muy implausibles. ¿Quién dijo que hacer buena ciencia tuviera que ser fácil?
.
6) El valor esperado de la funcion Vs(T,E) es igual a la "razón de probabilidad", p(T,E)/p(T), que a su vez es igual a la "razón de likelihood", p(E,T)/p(E). (Lo siento, pero la prueba de este teorema es un poco larga, y los que tengáis curiosidad la podréis ver en el libro Mentiras a medias, o en este artículo, (pgs., 356-357)). La noción matemática de "valor esperado" es aquí la misma que en el caso de Niiniluoto que vimos en la entrada tercera: cuál es el valor de Vs que esperaríamos en función de la probabilidad que E asigna a cada uno de los mundos posibles que son compatibles con E. Lo que significa este teorema es que la percepción de la verosimilitud de una teoría no es la misma cuando los científicos esperan que haya cambios importantes en E que cuando no lo esperan; en el primer caso, tenderán a considerar más razonable el valor esperado de Vs, mientras que en el segundo, tomarán E como (relativamente) "definitivo", y juzgarán las teorías directamente a través de Vs, no de su valor esperado. El caso es que las "razones" de probabilidad o likelihood son herramientas estadísticas habituales para la comparación de teorías, y el hecho de que nuestro modelo implique que eso ha de ser así es un punto a su favor.
.
7) Puede ocurrir que una teoría T' explique más hechos que otra T, pero parezca menos verosímil que ella. Este resultado tiene en cuenta la versión "c" del sentido de "aproximación" que indicamos en la entrada anterior: considerar la verosimilitud de una teoría como función de su coherencia con algún subconjunto de los hechos conocidos, no necesariamente todos. Esto ocurrirá, naturalmente, si T' explica más hechos Ei que T, pero la plausibilidad a priori de T' es mucho menor que la de T. Esto algo que suele ocurrir en las "revoluciones científicas" según Kuhn: el paradigma "nuevo" tiene menos anomalías que el "viejo", pero los defensores del viejo siguen defendiendo éste porque el paradigma nuevo les parece que hace supuestos intolerablemente implausibles.
.